CF506E 题解

一道极 (e) 妙 (xin) 的自动机优化 DP 的题目。

先假设最后得到的字符串为 \(T\)，由题意易知 \(T\) 合法当且仅当 \(T\) 是回文串且 \(S\) 是 \(T\) 的一个子序列。

\(T\) 是回文串的这个性质我们可以通过从外向内一个一个填字符来实现，所以我们需要 DP 的是 \(S\) 相对于 \(T\) 而言被匹配了多少个字符。

特别的，因为当 \(T\) 的长度为奇数的时候，最后一次填的字符本质上是一个字符，需要特别处理，所以下面我们先讨论 \(T\) 的长度为偶数的情况。

因为 \(T\) 这个字符串是从外向内确定的，所以 \(S\) 的匹配也是从外向内的，故可以设 \(f_{i,l,r}\) 表示考虑 \(T\) 的前后 \(i\) 个字符，当前 \(S\) 还剩下 \([l,r]\) 没有匹配到的方案数。

考虑转移，假设当前有 \(s[l] = s[r]\)，那么如果当前填的字符是 \(s[l]\)，就可以转移到 \(f_{i+1,l+1,r-1}\)，如果当前填的字符不是 \(s[l]\)，就可以转移到 \(f_{i+1,l,r}\)，转移系数为 \(25\)。

假设当前 \(s[l] \not= s[r]\)，那么如果当前填的字符是 \(s[l]\)，就可以转移到 \(f_{i+1,l+1,r}\)，如果当前填的字符是 \(s[r]\)，就可以转移到 \(f_{i+1,l,r-1}\)，如果当前填的字符不是两者，就可以转移到 \(f_{i+1,l,r}\)，转移系数为 \(24\)。

需要注意的是，对于所有的 \(f_{i,l,r}(l>r)\)，因为 \((l>r)\)，也就是说 \(S\) 已经被匹配完，所以无论填什么字符都没关系，那么它们就可以转移到 \(f_{i+1,l,r}\)，转移系数为 \(26\)。

这样我们便有了一个 \(n\times |S|^2\) 的 DP，如果把后面的状态强行剥离就可以做到 \(|S|^6\log n\)，似乎并没有什么用。

考虑优化这个 DP，我们把这个 DP 的转移用一张图来表示，对于 \(S=abab\)，转移图是这样的：

wftvp6.png

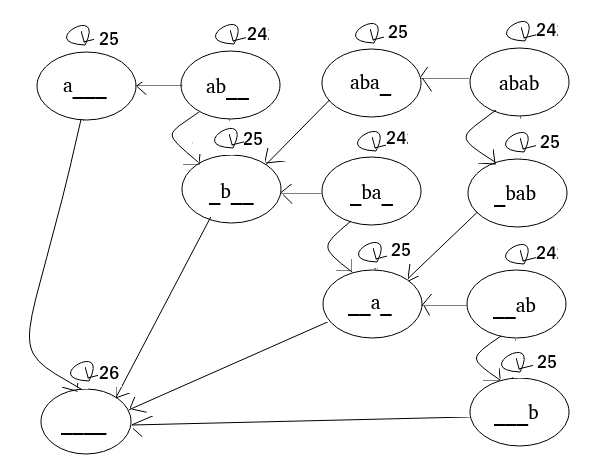
其中下划线是已经匹配的部分，在 \(i\) 行 \(j\) 列的椭圆表示 \(f_{x,i,j}\)，我们把所有的 \(l>r\) 的状态归到一个状态里面去，就有了如上的转移图。一个合法的方案本质上就是从 \(abab\) 走 \(n+|S|\) 步到 ____​ 的一条路径。

我们把某条路径上面的所有节点拿出来，并且按照 \(s[l]\) 是否等于 \(s[r]\) 分类成两种点，可以发现，无论这两种点的排列如何，当这两种点的数量确定的时候，答案已经确定了。

设 \(s[l]=s[r]\) 的点为 \(0\) 类点，\(s[l]\not=s[r]\) 的点为 \(1\) 类点，不难发现在某条路径上确定了 \(1\) 类点的数目后，可以直接计算得到一个唯一的 \(0\) 类点的数目，而 \(1\) 类点的数目的取值范围为 \([0,len-1]\)，所以总共不同的路径数最多只有 \(|S|\) 条。

考虑有多少种方案经过某条路径，设 \(g_{x,l,r}\) 表示在区间 \([l,r]\) 的这段转移中，总共经过 \(x\) 个 \(1\) 类点的方案数，用记忆化搜索即可求得，我们需要的就是 \(g_{x,1,|S|}\)。这部分复杂度 \(|S|^3\)。

在一条路径上面 DP 的复杂度是 \(|S|\times n\)，通过矩阵优化可以优化到 \(|S|^3\times \log n\)，总复杂度即 \(|S|^4\log n\)，虽然仍然过不了，但是优化了很多。

我们设起点为 \(S\)， \(0\) 类点为黑色，\(1\) 类点为白色，终点为 \(T\)，上述过程中的转移图差不多是这样：

w4aqtH.png

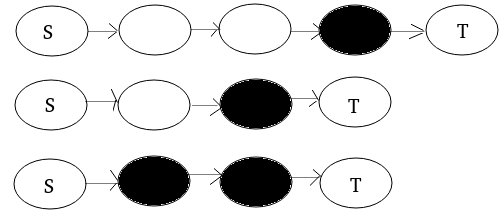
考虑继续优化，上述算法问题就出在我们对每种路径都跑了一次 DP，考虑把它们合并成一次。先规定所有的路径\(0\) 类点都在前面，\(1\) 类点都在后面。然后在新的转移图上把第一行放上 \(0\) 类点，第二行放上 \(1\) 类点，在第一行的点之间连边，第二行的点之间连边，现在就考虑怎么在第一行的点和第二行的点之间连边，不难发现，这种连边实质上代表了一种路径，因为这种边只能走一次，且走这种边就可以确定经过的 \(0\) 类点和 \(1\) 类点的数目，这样的话复杂度就优化到了 \(|S|^3\log n\)。

把上图按照这种优化连边之后的图就是这样：

w4d83R.png

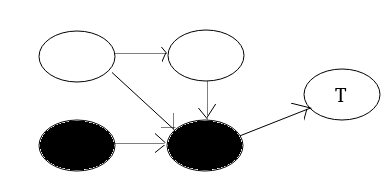
其中从第一行的点到第二行的点的转移系数为有多少种方案经过这种路径，即 \(g_{x,l,r}\)。可以发现这样转化之后只有 \(\frac{3}{2}|S|\) 个点，且因为转移图是 DAG 图，所以可以通过编号使得转移都是从编号小的点转移到编号大的点，这样可以得到一个比较优秀的常数优化。复杂度 \(|S|^3\log n\)。

最后还需要考虑一下 \(|T|\) 为奇数。我们先把 \(|T|\) 的长度看做 \(|T|+1\) ，这样就可以得到一个答案。考虑有多少种方案不合法，可以发现是所有最后一步是放两个字符，且恰好在最后一次转移的时候放的方案，我们把这种方案算出来减掉即可。具体的，把所有最后一步是放两个字符的路径拿出来，然后去掉终点的自环再跑一遍上述 DP，这次求出来的答案就是要减掉的方案。

至此便可完美解决此题。

代码如下：

#include <bits/stdc++.h>
#define debug(...) fprintf(stderr, __VA_ARGS__)
#define RI register int
typedef long long LL;

#define FILEIO(name) freopen(name".in", "r", stdin), freopen(name".out", "w", stdout);

using namespace std;

int const mod = 1e4 + 7;
char s[205];
int f[205][205][205];
int lim;
struct Matrix {
  int a[305][305];
  Matrix operator * (const Matrix &A) {
    Matrix re;
    for (RI i = 1; i <= lim; ++i)
      for (RI j = i; j <= lim; ++j) {
        re.a[i][j] = 0;
        for (RI k = i; k <= j; ++k)
          re.a[i][j] = (re.a[i][j] + a[i][k] * A.a[k][j]) % mod;
      }
    return re;
  }
} F;

Matrix Matpow(Matrix a, int k) {
  Matrix re;
  for (RI i = 1; i <= lim; ++i)
    for (RI j = 1; j <= lim; ++j)
      re.a[i][j] = (i == j);
  for (; k; k >>= 1, a = a * a)
    if (k & 1) re = re * a;
  return re;
}

int DP(int x, int l, int r) {
  if (x < 0) return 0;
  if (l >= r) return x == 0;
  if (f[x][l][r] != -1) return f[x][l][r];
  if (s[l] == s[r])
    f[x][l][r] = DP(x, l + 1, r - 1);
  else
    f[x][l][r] = (DP(x - 1, l + 1, r) + DP(x - 1, l, r - 1)) % mod;
  return f[x][l][r];
}

int main() {
  
#ifdef LOCAL
  FILEIO("a");
#endif

  memset(f, -1, sizeof(f));
  int n, len;
  cin >> (s + 1) >> n;
  len = strlen(s + 1);
  lim = len + (len + 1) / 2;
  for (RI i = 1; i <= len - 1; ++i) {
    F.a[i][i] = 24;
    F.a[i][i + 1] = (i != len - 1);
    F.a[i][lim - (len - i + 1) / 2] = DP(i, 1, len);
  }
  for (RI i = len; i < lim; ++i) {
    F.a[i][i] = 25;
    F.a[i][i + 1] = 1;
  }
  F.a[lim][lim] = 26;
  F = Matpow(F, (n + len + 1) / 2);
  int ans = 0;
  if (len != 1)
    ans = F.a[1][lim];
  ans = (ans + F.a[len][lim] * DP(0, 1, len) % mod) % mod;
  if ((n + len) & 1) {
    memset(F.a, 0, sizeof(F.a));
    for (RI i = 1; i <= len - 1; ++i) {
      F.a[i][i] = 24;
      F.a[i][i + 1] = (i != len - 1);
      if (!((len - i) & 1))
        F.a[i][lim - (len - i + 1) / 2] = DP(i, 1, len);
    }
    for (RI i = len; i < lim; ++i) {
      F.a[i][i] = 25;
      F.a[i][i + 1] = 1;
    }
    F = Matpow(F, (n + len + 1) / 2);
    if (len != 1)
      ans = (ans - F.a[1][lim] + mod) % mod;
    if (!(len & 1))
      ans = (ans - F.a[len][lim] * DP(0, 1, len) % mod + mod) % mod;
  }
  cout << ans << endl;

  return 0;
}

// created by Daniel yuan
/*
     ________
    /        \
   / /      \ \
  / /        \ \
  \            /
   \  ______  /
    \________/
*/