划分数就是把一个数 \(n\) 拆分成若干个正整数的和的方案数,其中这若干个正整数是无序的,也就是 \(\{1,1,2\}\) 和 \(\{1,2,1\}\) 是等价的拆分。
下面我们来讨论怎么求它。
简单 DP
我们可以设 \(f_{i,j}\) 表示把 \(i\) 拆分成 \(j\) 个正整数的方案数。
转移有两种,要么添加一个 \(1\),要么把所有数都加 \(1\)。
即 \(f_{i,j}=f_{i-1,j-1}+f_{i-j,j}\)。
那么我们要求的划分数就是 \(\sum_{x=0}^n f_{n,x}\)。复杂度 \(O(n^2)\)。
这个算法的优点是我们可以知道所有把 \(x\leq n\) 拆分成 \(y\leq n\) 个正整数的方案数,缺点是复杂度过高。
根号分治 DP
可以发现,大于 \(\sqrt{n}\) 的数我们最多选 \(\sqrt{n}\) 个,所以我们可以依靠这个来优化算法。
设 \(f_{i,j}\) 表示用小于等于 \(i\) 的数构成 \(j\) 的方案数。
转移有两种,要么是多加一个 \(i\),要么就把 \(i\) 加 \(1\)。
即 \(f_{i,j}=f_{i-1,j}+f_{i,j-i}\)。
这里的 \(i\) 我们只枚举到 \(\sqrt{n}\),这样我们就可以知道用小于等于 \(\sqrt{n}\) 拼成某个数的方案数。
设 \(g_{i,j}\) 表示用 \(i\) 个数大于 \(\sqrt{n}\) 的数构成 \(j\) 的方案数。
转移有两种,要么添加一个 \(\sqrt{n}+1\),要么把所有数都加 \(1\)。
即 \(g_{i,j}=g_{i-1,j-\sqrt{n}-1}+g_{i,j-i}\)。
因为大于 \(\sqrt{n}\) 的数我们最多用 \(\sqrt{n}\) 个,所以 \(i\) 的上限也是 \(\sqrt{n}\)。
那么最后的答案就是 \(\sum_{x=0}^n f_{\sqrt{n},x}\times \left(\sum_{y=0}^{\sqrt{n}} g_{y,n-x}\right)\) 。即枚举小于等于 \(\sqrt{n}\) 的数的和。复杂度 \(O(n\sqrt{n})\)。
这个算法的优点是比多项式做法容易,且复杂度优于简单 DP。缺点是我们只能求得 \(n\) 的划分数。
多项式
我们可以类似背包的来构造生成函数。
设 \(P\) 为划分数的生成函数,即 \(P_k\) 的系数为 \(k\) 的划分数。
那么就有 \(P=\prod_j^\infty\left(\sum_i a_ix^{ij}\right)\)。
即枚举选择的数的大小 \(j\),然后乘上它的生成函数。
根据常识,原式等于 \(\prod_{j=1}^\infty \frac{1}{1-x^j}\)。
然后通过 \(\ln\) 和 \(\exp\) 化乘为加,就可以求得 \(P\)。
我们先不看 \(\exp\),先算 \(\ln\)。那么原式就是 \(-\sum_{j=1}^\infty\ln(1-x^j)\)。
考虑怎么计算 \(\ln(1-x^j)\),换个元设 \(u=x^j\),我们就需要求 \(\ln(1-u)\)。
先求导,即 \(-\frac{1}{1-u}=-\sum_{i=0}^\infty u^i\),然后积分,即 \(-\sum_{i=1}^\infty \frac{u^i}{i}\) 。把元换回来,即 \(-\sum_{i=1}^\infty \frac{x^{ij}}{i}\)。
那么原式就成了 \(\sum_{j=1}^\infty \sum_{i=1}^\infty \frac{x^{ij}}{i}\)。
最后把这一坨 \(\exp\) 一下就得到了 \(P\)。
不难发现当上界为 \(n\) 的时候,这个求和的复杂度是 \(O(n\log n)\) 的。
而求 \(\exp\) 的复杂度也是 \(O(n\log n)\) 的,故总复杂度为 \(O(n\log n)\)。
这个算法的优点是能非常快的计算出 \(x\leq n\) 的划分数,缺点是很复杂,且对模数有要求。
至此就讨论完了三种求划分数的方法。但是如果你认为这就完了那就 too young too simple, sometimes naive 了,出题人怎么可能就只考裸的划分数呢。
下面我们再讨论一下如果限制了划分出来的正整数个数,或者限制了划分出来的正整数的大小该怎么做。
我们可以发现,上述算法的【简单 DP】是很好处理前者的,【多项式】是很好处理后者的,而【根号分治 DP】中的 \(f\) 可以维护后者, \(g\) 可以维护前者,合并都不好维护。但是回顾上述算法,你会发现它们在最根本的思想上是相似的,而它们在这方面的性质又不一样,这就促使了我们去探究上面两个限制的关系。
引理:把划分出来的正整数排序,并形成一个阶梯图,这个图在行列上具有对偶性。
这么说比较抽象,我也不知道表达对不对,但是看了下面的图就知道了。(只看加粗部分)
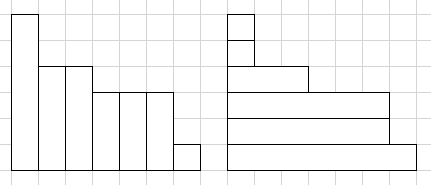
这张图不管是以列划分(左),还是以行划分(右),都可以看做是一个划分数的划分,且它们一一对应。
假设柱状物的个数为数的个数,柱状物的高度是数的大小。
那么如果限制是划分出来的正整数个数不超过数 \(x\) ,在左图相当于是柱状物的个数不超过 \(x\),那么在右图就是柱状物的高度不超过 \(x\)。
也就是说,限制划分出来的正整数个数不超过 \(x\),和限制划分出来的正整数的大小不大于 \(x\) 在本质上是相同的。我们可以对它们进行等价的转化。
这样就可以解释为何上述三个同根的算法性质不同了。