定义一个串 \(S\) 的划分 \(s_1,s_2...s_k\) 为回文划分当且仅当 \(s_1,s_2...s_k\) 都是回文串。
现在考虑求一个串 \(S\) 的回文划分数。\(1\leq |S| \leq 10^6\)。
为了方便,我们定义字符串下标从 \(1\) 开始,且 \(S[l:r]\) 为字符串 \(S\) 中 \(s[l],s[l+1]...s[r]\) 这个子串。
考虑设 \(f[i]\) 表示 \(i\) 结尾的这个前缀的回文划分方案数。
转移显然,即 \(f[i]=\sum f[i-L]~(S[i-L+1:i] \text{是回文串})\)。
如果枚举 \(i,L\) 再暴力判断,复杂度会达到严格 \(O(|S|^3)\),如果用一些方法预处理快速判断一个串是不是回文串,可以做到严格 \(O(|S|^2)\)。
考虑优化,对于快速找到回文 Border,可以使用回文自动机,这样每次在当前节点跳 \(parent\) 边跳到的都是回文后缀,这样就可以直接转移。复杂度是 \(O(\sum_i \text{以 i 结尾的回文后缀个数})\),在随机数据下跑得很快。但是这样显然可以被 \(aa...aa\) 卡到 \(O(|S|^2)\)。故考虑进一步优化。
引理 \(1\) : 对于一个串 \(S\) 的所有长度大于 \(\frac{|S|}{2}\) 的回文 Border,它们的长度形成一个等差数列。
证明:拿出最长的回文 Border \(T\),那么 \(S\) 就存在周期 \(|S|-|T|\),所以长度为 \(|S|-2(|S|-|T|)\) 的这个后缀也是一个回文 Border,长度为 \(|S|-3(|S|-|T|)\) 的这个后缀也是一个回文 Border……把这一组 Border 去掉之后,剩下的回文 Border 长度一定小于等于 \(\frac{|S|}{2}\),不然的话 \(T\) 就不会是最长的回文 Border。
这样在 DP 中可以转移的点也可以被分成 \(\log_2|S|\) 个等差数列。我们就可以这么做:预处理 \(F[i][j]\) 表示 \(f[i]+f[i-j]+...\),那么对于一个等差数列,如果其公差小于一个阈值,就直接查表,否则暴力跳。这样复杂度上限可以被优化到 \(O(|S|\sqrt{|S|\log_2|S|})\),实际效率未知。
我们把某个等差数列拿出来,看看它有什么性质。
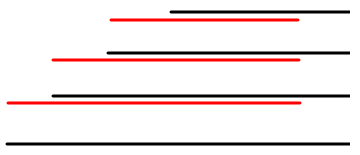
这是 \(4\) 个形成等差数列的 Border。
我们把每个 Border 按照比恰好比它长的 Border 的回文中心对称过去,可以发现它的开头是恰好比它长的 Border 的开头,结尾都在同一个位置。
如果设 \(g[x]\) 为在回文自动机上以 \(x\) 为末项的回文 Border 的 \(\sum f\),把上图的串从上到下依次编号成 \(1,2,3,4\),那么我们可以发现,对于现在要求的 \(g[4]\),有很大一部分已经被 \(g[3]\) 算过了(\(g[3]\) 即红色条纹部分,\(g[4]\) 即黑色条纹部分),因为我们到现在这个位置计算 \(g[4]\) 时,一定会先走过计算 \(g[3]\) 的位置。所以就只需要使 \(g[4]=g[3]\) 且把 \(g[4]\) 额外加上【除掉当前等差数列最小的 Border 的那个 \(f\) 】即可。
这样就可以在 \(O(n\log_2 n)\) 的时间内解决该题。
直接讨论回文划分太抽象了,举个具体例子。
CF932G Palindrome Partition
给定一个串 \(S\),把串分为偶数段。
假设分为了 \(s_1,s_2,s_3....s_k\)。
求,满足 \(s_1=s_k,s_2=s_{k−1}.....\) 的方案数。
\(2\leq |S| \leq 10^6\),方案数对 \(10^9+7\) 取模。
Solution:
乍一看这个题和回文划分没有什么关系,但是我们不妨分析一手。
为了方便,我们定义字符串下标从 \(1\) 开始。
考虑逐个考虑 \(s_1\) 和 \(s_k\),\(s_2\) 和 \(s_{k-1}\) 这样的匹配对。我们发现当剩余串的长度固定的时候,留下的是中间某一个固定的段,这样就不是很好,因为我们很难得到中间某个串的信息。所以尝试把这个串修改一下使得每次分段都是一个连续的区间,即改成 \(s[1]s[n]s[2][n-1]...\),这样我们就可以发现,对于一个分段,它都是一个长度为偶数的连续区间,且该串为回文串。
这样问题就转化成了:把一个串 \(S\) 分解成若干个长度为偶数的回文串的方案数。直接用上面的算法做即可。
代码如下:
1 |
|