一些神题。
[SDOI2019]热闹的聚会与尴尬的聚会
给一张 \(n\) 点 \(m\) 边的无向图。选出两个点集 \(S\), \(T\),\(S\) 没有要求,\(T\) 需要满足其中任意两点没有边,\(S\), \(T\) 之间没有限制。设 \(val(S)\) 为仅保留 \(S\) 的点和 \(S\) 的点之间的边的最小度数的点的度数,\(val(T)=|T|\)。构造一种满足 \(\lfloor \frac{n}{val(S)+1} \rfloor\leq val(T)\) 且 \(\lfloor \frac{n}{val(T)+1} \rfloor\leq val(S)\) 的方案。\(T\) 组询问。\(T\leq 32,n\leq 10^4,m\leq 10^5\)。
考虑贪心。每次选择度数最小的点,把它加入 \(T\),然后删去所有与 \(T\) 连边的点,并更新所有点的度数。
设每次删除时的度数为 \(deg\),那么就有 \(\sum_{i=1}^T deg_i=n-|T|\)。
而对于 \(S\),在某个时刻直接把剩下的点全部取出来,最优是 \(\max\{deg_i\}\) 的。
\(val(S)\) 最劣的时候就是所有的 \(deg\) 都均分,即 \(\lceil\frac{n-|T|}{|T|}\rceil\)。这样仍然是满足要求的。
所以直接用个数据结构动态维护 \(deg\) 即可,复杂度 \(O(T\times (m\log n))\)。
CF1174F Ehab and the Big Finale
这是一道交互题。
你有一棵 \(n\) 个节点的有根树,\(1\) 号点是根节点。
这棵树中有一个隐藏的节点 \(x\),你需要通过询问把 \(x\) 找出来。
你可以进行如下两种询问:
1、d u \((1\le u\le n)\)。交互库会返回节点 \(u\) 和 \(x\) 的距离。
2、s u \((1\le u\le n)\)。交互库会返回从 \(u\) 到 \(x\) 的路径上第二个点的标号。注意,你询问的 \(u\) 必须是 \(x\) 的祖先,否则会报错。
你需要在不超过 \(36\) 次询问之内找出 \(x\)。\(x\) 是预先设定好的,不会随着询问而改变。\(n \le 2\times 10^5\)。
先询问 d 1 得到候选点集合,设其大小为 \(cnt\)。
每次把当前考虑的点移动到候选点结合的 LCA。
然后求一遍子树候选点集合大小。如果当前点 \(x\) 没有一个集合大小大于 \(\frac{cnt}{2}\) 的儿子,那么直接问 s x 就可以把候选点的数量减半。否则往哪个唯一的集合大小大于 \(\frac{cnt}{2}\) 搜,每次往重儿子走,直到走到一个候选点 \(y\),然后询问 d y,这时候所有的候选点都可以与 \(y\) 求距离然后判断是否还是候选点。假设之后的候选点集合的 LCA 为 \(z\),因为 \(y\) 是 \(z\) 走重儿子走到的,所以在极端情况下 \(z\) 还有两个儿子,且大小各为 \(\frac{cnt}{3}\),所以此时问 s z 就可以把候选点数量减至至多 \(\frac{n}{3}\)。
综上复杂度是 \(2\log_{3}n\) 的,完全三叉树可以卡到此复杂度上限。
CF750F New Year and Finding Roots
这是一道交互题。
有一棵高度为 \(h\) 的有根完全二叉树,点的编号从 \(1\) 到 \(2^h-1\)。每一次你可以询问某一个点在树上的邻居,现在请你使用不超过 \(16\) 次询问找到树根。\(T\) 组数据,\(T\leq 500,2\leq h \leq 7\)。
假设当前在叶子。
直接跳到其父亲,那么我们可以直接得到当前点的深度,设为 \(dep\)。
然后询问一次,然后随机在两个出边之间选一条走,如果走错了,那么就会花 \(h-dep\) 次走到叶子,这时候这两条出边的另一个就是跳向父亲的。
当 \(h=7\) 的时候脸足够黑的话要 \(22\) 次,即主链上 \(7\) 次,支链上 \(\sum_{i=1}^6i=15\) 次。
不难发现越高的点不小心走错花的贡献越多。我们不希望走错,所以考虑当深度足够浅的时候 BFS——这样我们就不存在走错了。
当这个阈值为 \(3\) 的时候,我们可能查询的点只有 \(17\) 个,如图所示:
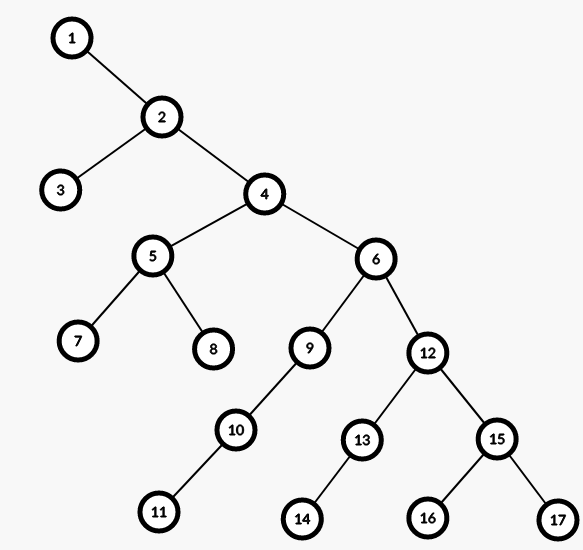
在 \(6,12,15,17\) 我们采取 DFS 的策略,在 \(4\) 我们就开始 BFS。
这样一共有 \(17\) 个点,看似超出了一次,但实际上这 \(17\) 个点中一定有根,如果前 \(16\) 次询问都没问到根,那么最后剩下的就一定是根。
实际上我们并不需要找叶子。我们随机一个点,然后随机走直到走到了叶子,这时候我们可以通过路径长度来确定一个深度比较浅的点。如上图如果我们一开始走的 \(10\sim 14\),那么我们就可以直接确定 \(6\) 号点的深度 \(4\),因为深度大于 \(4\) 的点走不出一个长度为 \(6\) 的路径。
不难发现这样确定点不会劣于从叶子开始的做法。故 \(16\) 次足够了。
CF1368F Lamps on a Circle
这是一道交互题。
Alice 和 Bob 在玩游戏,有 \(n\) 盏灯排成一个圈,顺时针标号为 \(1\sim n\),初始所有灯都是关着的。
每轮操作为:
- Alice 选择一个 \(k\in [1,n]\) 然后打开任意 \(k\) 盏灯(可以重复打开)。
- Bob 关闭一段长度为 \(k\) 的连续区间的灯。
Alice 可以在每轮开始时选择停止游戏,这局游戏的得分就是当前亮着的灯的数量。
Alice 想要最大化得分,Bob 想要最小化得分。
你需要使用不超过 \(10^4\) 次操作达到得分上界。
\(n\le 1000\)。
假设我们把序列分成若干段,相邻之间有至少一个空位,那么最后的答案就是 \(\sum size-\max size\)。
因为你在修改的时候,如果至少有二个段,Bob 就不能把你所有的修改都抵掉。所以你最后总会剩且只剩一段,而 Bob 也总能把你企图修改的最大的一段的变回来。
假设你要分 \(x\) 段,那一定是平均分最优。所以可以直接枚举段数求该段数下的贡献。
每一轮 Alice 都可以多点亮至少一个灯,所以 \(10^4\) 足够了。